揭秘傅里叶变换：探究其深刻的物理意义

在探索自然界的奥秘时，科学家们常常需要借助各种数学工具来揭示物理现象的本质。傅里叶变换就是这样一种强大的数学工具，它在物理学、工程学以及众多应用领域中发挥着不可替代的作用。那么，傅里叶变换的物理意义是什么呢？让我们一起揭开这个神秘的面纱。

傅里叶变换的基本定义

首先，让我们简要了解一下傅里叶变换的基本定义。傅里叶变换（Fourier Transform）是一种数学变换方法，用于将一个函数从时间域（或空间域）转换到频率域。在时域中，信号是时间的函数，描述信号随时间的变化；而在频域中，信号是频率的函数，描述了信号在不同频率上的组成。简单来说，傅里叶变换就像是一位翻译，将时间域或空间域中的信号转换为频率域中的表示。

傅里叶变换的物理意义

傅里叶变换的物理意义在于它揭示了信号的频率特性。这种转换不仅有助于我们更好地理解和分析信号，还为信号的处理提供了极大的便利。

1. 信号分解与合成

傅里叶变换的核心思想是将一个复杂的信号表示为多个不同频率的正弦波和余弦波的叠加。这意味着，任何复杂的信号都可以通过分解成若干个简单的正弦波（或余弦波）来进行分析。这种表示方式将一个复杂的时间域函数转换为了一个简单的频域函数，便于我们进行后续的处理和分析。

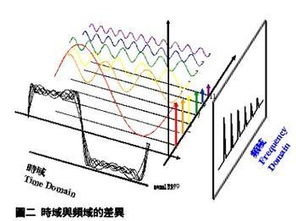
想象一下，一个复杂的音乐信号，它可能包含了多种不同的音调和音色。通过傅里叶变换，我们可以将这个复杂的音乐信号分解成若干个不同频率的正弦波，每个正弦波对应一个特定的音调。这样，我们就可以清晰地看到每个音调的频率、幅度和相位信息，从而更准确地理解音乐的组成。

2. 信号频谱分析

傅里叶变换揭示了信号的频率特性，使我们能够通过分析信号的频谱来更好地理解和处理信号。频谱是信号在频率域上的表示，它显示了信号在不同频率上的能量分布。

在音频处理中，傅里叶变换可以用于分析音频信号的频谱特性。通过频谱分析，我们可以了解音频信号中各个频率成分的强度，进而进行噪声滤除、音效增强等操作。例如，在降噪耳机中，利用傅里叶变换可以精确地识别并去除环境中的噪声，同时保留音乐信号中的有用成分。

在图像处理中，傅里叶变换同样可以用于图像的频域滤波、特征提取等任务。通过频谱分析，我们可以观察到图像中不同频率的成分，进而进行频率滤波、图像增强、减少噪声等操作。

3. 信号处理中的应用

傅里叶变换在信号处理中的应用非常广泛，涵盖了音频处理、图像处理、通信系统等多个领域。

音频处理：通过傅里叶变换，我们可以分析音频信号的频谱特性，进行噪声滤除、音效增强等操作。此外，在音频编码和解码中，傅里叶变换也发挥着重要作用。

图像处理：在图像处理中，傅里叶变换可以用于图像的频域滤波、特征提取、图像压缩等任务。例如，在JPEG图像压缩中，傅里叶变换被用于将图像编码成频域数据以实现压缩。

通信系统：在通信系统中，傅里叶变换可以将信号转换到频率域，进行调制、解调、频谱分析等操作。例如，正交频分多路复用技术（OFDM）就是基于傅里叶变换将高速数据流分成多个低速子流，并在不同频率上传输，从而高效利用频谱资源和抵御多径干扰。

4. 物理现象的频率分析

傅里叶变换不仅在信号处理中发挥着重要作用，它还是一种广泛应用的数学工具，不同物理现象能通过傅里叶变换转换到频率域进行分析。

在物理学中，许多自然现象都可以用频率来描述和分析。例如，在波动理论中，波动可以看作是由一系列不同频率的正弦波叠加而成的。通过傅里叶变换，我们可以将这些复杂的波动信号分解成若干个不同频率的正弦波，从而更准确地理解波动的特性。

此外，在量子力学、光学等领域中，傅里叶变换也发挥着重要作用。例如，在量子力学中，波函数的傅里叶变换可以揭示粒子的动量分布；在光学中，通过傅里叶变换可以分析光的干涉和衍射现象。

傅里叶变换的优越性和局限性

傅里叶变换之所以能够在众多领域中得到广泛应用，离不开其优越的数学性质和物理意义。然而，傅里叶变换也存在一定的局限性。

优越性

线性算子：傅里叶变换是线性算子，若赋予适当的范数，它还是酉算子。这意味着傅里叶变换满足线性叠加原理，可以方便地处理线性系统。

逆变换易求：傅里叶变换的逆变换容易求出，而且形式与正变换非常类似。这使得我们可以方便地通过傅里叶逆变换将频域信号转换回时域信号。

卷积定理：著名的卷积定理指出，傅里叶变换可以化复杂的卷积运算为简单的乘积运算。这提供了计算卷积的一种简单手段，在信号处理等领域中具有重要意义。

快速算法：离散形式的傅里叶变换可以利用数字计算机快速地算出（其算法称为快速傅里叶变换算法（FFT））。这使得傅里叶变换在实时信号处理等应用中成为可能。

局限性

尽管傅里叶变换具有诸多优越性，但它也存在一定的局限性。例如，在时域中突变的信号在频域中会产生较宽的频谱分量，即所谓的“频谱泄漏”现象。此外，对于非周期信号或有限长信号，傅里叶变换的结果可能包含无穷多个频率分量，这在实际应用中是不现实的。为了克服这些局限性，科学家们提出了多种改进方法，如窗函数法、短时傅里叶变换等。

结语

傅里叶变换作为一种强大的数学工具，在物理学、工程学以及众多应用领域中发挥着不可替代的作用。它通过将一个复杂的信号表示为多个不同频率的正弦波和余弦波的叠加，揭示了信号的频率特性，使我们能够更好地理解和处理信号。无论是在音频处理、图像处理还是通信系统中，傅里叶变换都发挥着重要作用。尽管它存在一定的局限性，但随着科学技术的不断发展，我们相信傅里叶变换将在未来继续展现出其巨大的潜力和价值。