几何体的分类概览

在探索数学与空间的奇妙交汇中，几何体作为构成这一宏伟殿堂的基本砖石，承载着无尽的魅力与奥秘。它们不仅仅是抽象概念的载体，更是连接现实世界与数学逻辑的桥梁。对于那些对几何体世界充满好奇的你来说，本文将带你踏上一场发现之旅，一窥几何体的多样分类及其背后的精彩故事。

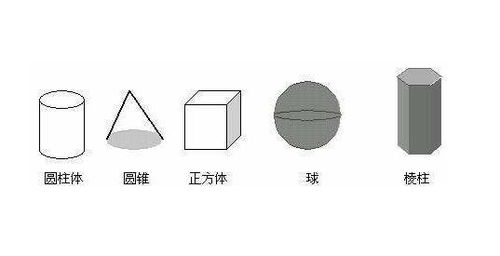
平面几何体与立体几何体

几何体的分类首先可以从维度上划分为两大类：平面几何体与立体几何体。平面几何体存在于二维平面上，而立体几何体则占据三维空间。

平面几何体

点：作为几何学的最基本元素，点没有大小、形状或维度，仅代表位置。

直线：由无数个点组成，沿一个方向无限延伸，宽度为零。

线段：直线的一部分，有两个明确的端点，长度有限。

射线：从一个点出发，沿一个方向无限延伸的直线部分。

圆：所有到中心点的距离相等的点的集合，形成闭合曲线。

多边形：由三条或更多直线段首尾相连围成的封闭图形，如三角形、四边形（包括正方形、矩形）、五边形等。

立体几何体

立体几何体，或称空间几何体，是三维空间中的实体，具有长度、宽度和高度。

多面体：由平面多边形围成的立体图形。

正多面体：所有面都是全等的正多边形，且所有顶点处相同数量的面相交，如正四面体（4个正三角形面）、正六面体（正方体，6个正方形面）、正八面体（8个正三角形面）、正十二面体（12个正五边形面）和正二十面体（20个正三角形面）。

棱柱：两个平行且相等的多边形底面，侧面为矩形或平行四边形的立体。

棱锥：有一个多边形底面，其余面为有一个公共顶点的三角形侧面的立体。

旋转体：由一个平面图形绕其边或轴上的一点旋转一周形成的立体。

圆柱：矩形绕其一边旋转而成，有两个平行且相等的圆面作为底面。

圆锥：直角三角形绕其一直角边旋转而成，有一个圆形底面和一个顶点。

球体：所有点距球心距离相等的点的集合，形成完美的三维对称体。

圆环体：两个平行且不相交的圆面通过侧面连接而成的立体，类似于甜甜圈形状。

特殊几何体

除了上述基本分类，还有一些特殊的几何体，它们在特定领域或应用中展现出独特价值。

超立方体（四维立方体）：虽然难以在三维空间中完全可视化，但超立方体是立方体在四维空间的推广，拥有8个立方体“面”。

曲面几何体：如球面、抛物面、双曲面等，它们不是由平面多边形构成，而是由连续变化的曲线面组成。

分形几何体：展现出自相似性的复杂几何形状，如曼德博集合、谢尔宾斯基三角等，它们挑战了传统几何学的界限，揭示了自然界的复杂之美。

几何体的应用与意义

几何体不仅在数学研究中占据核心地位，而且在建筑、艺术、工程、物理等多个领域发挥着不可替代的作用。

建筑设计：从古希腊的帕特农神庙到现代的摩天大楼，几何体的运用赋予了建筑物稳定、和谐的美感。

艺术创作：雕塑家通过几何体的组合与变形，创造出富有表现力的三维作品；画家则利用透视原理，在二维平面上表现三维空间的深度。

工程技术：机械设计、航空航天、土木工程等领域，几何体的精确计算与优化设计是提高效率、确保安全的关键。

物理研究：量子力学中的波函数、广义相对论中的时空曲率，都以抽象而复杂的几何形式揭示了自然界的本质。

探索未知，激发想象

几何体的世界远不止于此，随着数学理论的深入和科技的进步，人类对几何体的认知不断拓展。从非欧几里得几何的奇异空间，到超弦理论中的高维时空结构，几何体作为探索宇宙奥秘的工具，激发着人类无限的想象力与创造力。

对于那些渴望深入了解几何体分类的你，每一次探索都是一次思维的飞跃，一次对未知世界的勇敢迈进。不妨拿起笔和纸，亲手绘制这些几何体，感受它们的形态之美；或者利用计算机软件，模拟出那些难以想象的高维空间。在这个充满奇迹的几何世界里，每个人都能成为自己的探险家，发现属于自己的几何宝藏。

几何体，作为连接现实与抽象、简单与复杂的桥梁，等待着每一位好奇的心灵去触碰、去理解、去创造。在这个旅程中，你将不仅学会识别与分类，更重要的是，你将学会如何以几何的视角观察世界，用数学的语言解读宇宙的奥秘。