探索双曲线：揭秘其神秘的渐近线方程

在数学的浩瀚宇宙中，双曲线以其独特的形状和性质吸引着无数探索者的目光。对于那些对几何世界充满好奇，尤其是想要深入了解双曲线奥秘的你来说，双曲线的渐近线方程无疑是一个引人入胜的话题。今天，就让我们一同揭开双曲线渐近线的神秘面纱，探索它背后的数学之美。

双曲线：几何的韵律

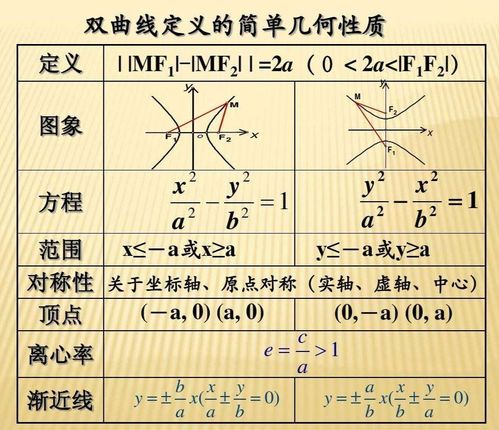
双曲线，这个在平面上由两条无限延伸、永不相交的曲线组成的图形，自古以来就激发着数学家的好奇心。不同于椭圆的闭合与和谐，双曲线以其开放和无界展现出一种独特的动态美。在笛卡尔坐标系中，双曲线通常由形如x²/a²-y²/b²=1（a,b>0）的方程定义，其中a和b是两个正实数参数，决定了双曲线的形状和大小。

渐近线：无限接近的边界

当我们观察双曲线时，会发现随着x值的增大或减小，y值似乎趋向于某个特定的直线。这些直线，就是我们所说的双曲线的渐近线。渐近线并不是双曲线的一部分，但它们与双曲线有着密切的关系——双曲线的两支无限接近这些直线，但永远不会相交。渐近线为双曲线提供了一个“视觉边界”，帮助我们在视觉上把握双曲线的整体形态。

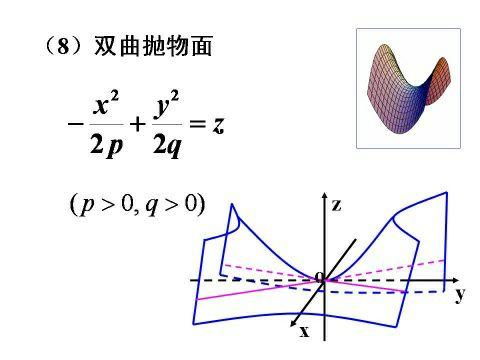
推导渐近线方程：数学的探索之旅

要理解双曲线的渐近线方程，我们可以从双曲线的基本方程出发。考虑标准形式的双曲线方程x²/a²-y²/b²=1，我们可以尝试通过令等式右边趋近于0来找到渐近线的方程。这背后的逻辑是，当x的值变得非常大时，x²/a²的值将远大于y²/b²，因此y²/b²项的影响相对于x²/a²项来说可以忽略不计。

1. 水平渐近线：对于双曲线来说，由于其开放的性质，实际上并没有水平渐近线（即y=常数）。随着x的增大或减小，y的值也在不断变化，没有趋于某个固定值的趋势。

2. 斜渐近线：这是双曲线最为显著的渐近线类型。为了找到斜渐近线的方程，我们可以将双曲线方程改写为y的形式：

y = ±b/a * √(x²/a²) * √(1 + (a²/b²) * (1 - x²/a²))

当x非常大或非常小时，我们可以近似地认为x²/a²远大于1，因此(1 - x²/a²)项相对于x²/a²来说可以忽略。于是，上式可以简化为：

y ≈ ±b/a * √(x²/a²) * √(1) = ±b/a * x/a = ±(b/a)x

这里，我们得到了双曲线的两条斜渐近线的方程：y = ±(b/a)x。这两条直线在视觉上“框定”了双曲线的两支，尽管它们并不真正属于双曲线的一部分。

渐近线的几何意义与应用

渐近线不仅在数学上具有理论价值，还在实际应用中发挥着重要作用。在物理学、工程学、经济学等多个领域，双曲线及其渐近线的概念被广泛运用。

物理学：在光学中，光线经过特定形状的镜面反射后形成的路径可能与双曲线有关，其渐近线可以帮助我们理解光线的传播方向。

工程学：在桥梁设计、天线形状优化等方面，工程师可能会利用双曲线的性质来设计结构，以达到最佳的稳定性和效率。渐近线为这些设计提供了一个直观的参考框架。

经济学：在某些经济模型中，如生产函数、成本曲线等，双曲线的形状和渐近线可能用来描述资源分配、产量增长等经济现象的趋势。

渐近线的艺术魅力

除了科学应用外，双曲线的渐近线还蕴含着一种独特的艺术美感。在艺术创作中，设计师们常常利用双曲线的渐近线来创造具有动态感和深度感的视觉效果。无论是建筑设计中的流线型外观，还是平面设计中的视觉引导线，双曲线的渐近线都能以其优雅的曲线和无限延伸的特质，为作品增添一份神秘与魅力。

结语：探索未尽，魅力永恒

双曲线的渐近线方程，作为连接数学理论与现实世界的桥梁，不仅揭示了双曲线这一几何图形的内在规律，也为我们打开了一扇通往无限想象与创造的大门。无论是对于数学爱好者、科学家、工程师，还是艺术家而言，双曲线的渐近线都是一个值得深入探索和欣赏的主题。它教会我们，即使在看似复杂和抽象的数学世界中，也隐藏着简洁、和谐与美的真谛。

随着我们对双曲线及其渐近线的理解不断加深，相信未来会有更多令人惊叹的发现和应用等待着我们去挖掘。在这个过程中，让我们保持一颗好奇和敬畏的心，继续在数学的海洋中航行，探索那些未知而迷人的领域。因为，正是这份对未知的追求和探索，让我们的生活变得更加丰富多彩，也让人类的智慧之光在宇宙的黑暗中熠熠生辉。