探究维纳过程的定义与特性

维纳过程，作为随机过程理论中的一个核心概念，是现代概率论与随机分析的重要组成部分。它起源于物理学中对布朗运动的数学描述，随后在金融数学、信号处理、生物统计学等多个领域展现出广泛的应用价值。本文旨在通过一系列关键词，如“随机游走”、“连续时间随机过程”、“独立增量性”、“正态分布”、“鞅性质”等，深入探讨维纳过程的本质特征、数学定义、性质以及其在不同领域的应用实例。

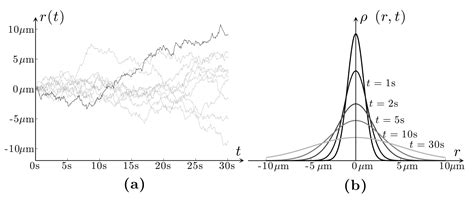
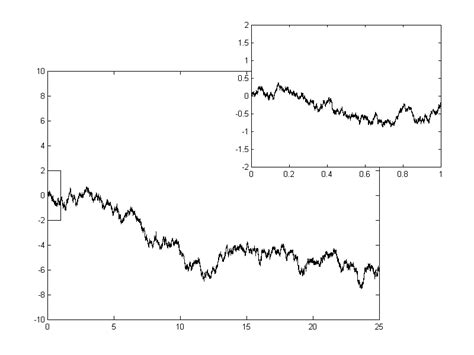
首先，从随机游走谈起，这是理解维纳过程的一个直观起点。随机游走，简而言之，是一个物体在每一步随机选择方向并移动固定距离的过程。在一维空间中，这可以想象为粒子在直线上左右跳跃。如果将时间连续化，并将每一步的跳跃距离缩小至无穷小，同时保持跳跃频率（即单位时间内的跳跃次数）趋于无穷大，那么这种离散时间的随机游走过程将趋于一个连续时间的随机过程——维纳过程。

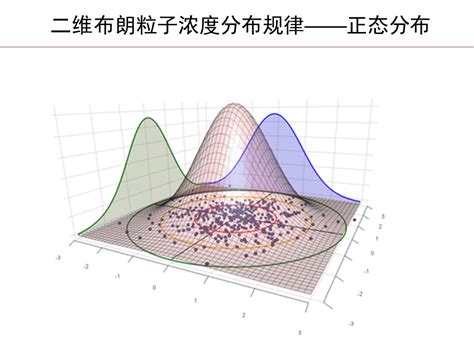
维纳过程，正式定义为连续时间随机过程W(t)，t≥0，满足以下性质：

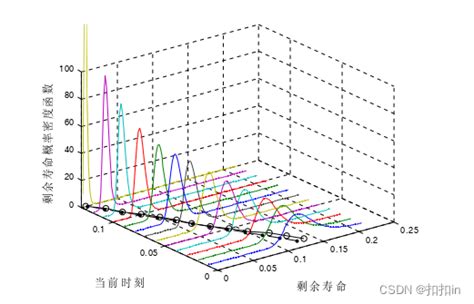
1. W(0)=0，即过程从原点开始。

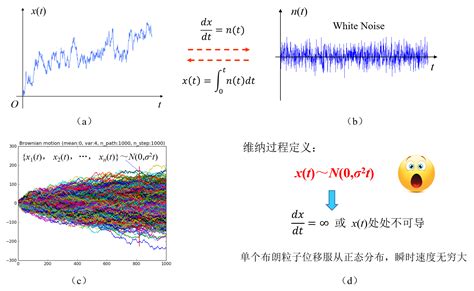
2. W(t)具有独立增量性，意味着对于任意0≤t1

3. 对于任意0≤s

4. W(t)的路径是连续的，但不可微（即其导数不存在）。

这些性质共同刻画了维纳过程作为连续时间随机游走的本质。其中，独立增量性和正态分布的假设保证了过程的随机性和平稳性；而连续性则反映了物理世界中许多现象的连续性变化特征。不可微性则揭示了维纳过程路径的极端不规则性，这种不规则性在数学上表现为其路径的“无处可微”，即在任何时间点附近，路径的斜率都是不存在的。

进一步地，维纳过程还展现出一种特殊的数学结构——鞅性质。在概率论中，鞅是一种具有特定条件的随机过程，其特点是在给定过去信息的条件下，未来的期望值保持不变。对于维纳过程W(t)，可以证明在适当的数学框架下，它满足鞅性质。这一性质在金融数学中尤为重要，因为它与无套利定价理论紧密相连，为衍生品定价提供了理论基础。

在金融领域，维纳过程（或其变种，如几何布朗运动）被广泛用于模拟股票价格等金融资产的波动。通过将股票价格视为一个维纳过程加上一个漂移项（代表资产的平均增长率），可以构建出著名的布莱克-斯科尔斯期权定价模型。该模型不仅为金融衍生品（如期权、期货等）的定价提供了数学工具，还推动了量化投资、风险管理等领域的发展。

除了金融数学，维纳过程在信号处理、生物统计学等领域也有重要应用。在信号处理中，维纳过程可用于建模噪声信号，特别是那些具有高斯白噪声特性的信号。通过利用维纳过程的性质，可以设计出有效的滤波算法，从含噪信号中提取出有用信息。在生物统计学中，维纳过程被用于描述生物体内某些指标（如血糖浓度、血压等）的随机波动，为疾病诊断、预后评估等提供了数学支持。

此外，维纳过程还与偏微分方程、随机积分等数学分支有着密切的联系。例如，通过引入伊藤积分，可以定义维纳过程关于时间的积分，进而研究由维纳过程驱动的随机微分方程。这些方程在物理学、工程学等领域中具有重要的应用价值，如描述粒子的随机运动、系统的随机稳定性等。

值得注意的是，尽管维纳过程在许多领域都取得了显著的成功，但它也面临着一些挑战和限制。例如，维纳过程的正态分布假设可能无法完全捕捉某些实际现象的复杂性和非线性特征。为了克服这些限制，研究者们提出了许多扩展和变种模型，如分数维纳过程、跳跃-扩散过程等，以更好地适应不同领域的需求。

综上所述，维纳过程作为随机过程理论中的基石之一，不仅具有深厚的数学基础，还在多个领域展现出广泛的应用前景。通过深入理解维纳过程的性质和应用，我们可以更好地把握随机现象的本质规律，为科学研究和技术创新提供有力的数学支持。未来，随着数学理论的不断发展和应用领域的不断拓展，维纳过程及其相关模型将继续在各个领域发挥重要作用，推动人类社会的进步和发展。