平面定义详解：轻松理解平面概念

在探索几何学的广阔领域中，平面的概念是构建一切理论知识与实践应用的基石。它不仅是数学学科中的一个基础要素，还广泛渗透于物理、工程、设计乃至日常生活的方方面面。本文旨在深入浅出地解析平面的概念，带领读者走进这一看似简单实则深邃的几何世界。

一、平面的直观认识

提到“平面”，我们的脑海中或许会立刻浮现出一张白纸、一面墙壁或是平静的湖面等形象。这些实例虽然具体，但不足以全面定义平面。在几何学中，平面是一个抽象而无限延展、没有厚度、无边界且完全平坦的二维空间。它超越了物理世界的限制，是一个理想化的数学模型。

二、平面的数学定义

从数学角度来看，平面可以通过以下两种方式定义：

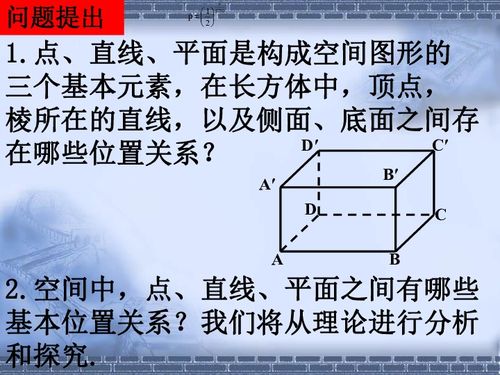
1. 三点确定一个平面：任意不共线的三点可以确定一个唯一的平面。这意味着，如果在空间中选取任意三个不位于同一直线上的点，它们将共同界定一个平面，且该平面是唯一的。

2. 向量与方程表示：在解析几何中，平面可以通过一个法向量和一个点来确定。若已知平面上的一个点P(x0, y0, z0)和一个与该平面垂直的法向量n(a, b, c)，则该平面可由以下方程表示：ax + by + cz - (ax0 + by0 + cz0) = 0。此方程刻画了平面内所有点的集合，其中法向量n决定了平面的方向性。

三、平面的性质

平面具有一系列独特的性质，这些性质构成了平面几何学的核心内容：

平坦性：平面内任意两点之间的连线都是直线，且平面内不存在曲率。

无限延展性：平面没有边界，可以向任意方向无限延伸。

平行性与相交性：两个平面可以平行（即永不相交）或相交于一条直线。

两点确定一条直线：在平面内，任意两个不同的点可以确定一条唯一的直线。

直线的分类：在平面中，直线可以是无限的、有起点的射线或两端都有终点的线段。

角度与距离：平面内可以测量两点之间的距离以及两条直线或线段之间的夹角。

四、平面的应用实例

平面的概念在现实生活与科学技术中发挥着至关重要的作用：

建筑设计：建筑师利用平面图纸设计建筑布局，确保结构的功能性和美观性。平面几何原理如对称性、比例关系等在设计过程中被广泛应用。

地图制作：地理信息系统（GIS）和地图制作中，地球表面被投影到平面上，以简化表示和分析。虽然这种投影会引入一定的变形，但仍是研究地理空间分布的有效工具。

计算机图形学：在计算机生成的图像和视频中，平面是构建三维场景和二维界面的基础。通过算法模拟平面、光线和阴影的相互作用，创造出逼真的视觉效果。

物理学：在物理学中，特别是在力学和电磁学领域，平面常被用来描述物体的运动轨迹、力的分解与合成等。例如，在研究物体的滑动、滚动或抛体运动时，平面的概念尤为重要。

印刷与出版：平面设计是视觉传达的重要分支，涉及书籍、杂志、广告、标志等多种媒介。设计师通过色彩、字体、图片和布局的巧妙组合，在平面上传达信息、激发情感。

五、平面的高级概念

随着学习的深入，我们会发现平面几何中还隐藏着更多复杂而迷人的概念：

平面内的几何变换：包括平移、旋转、缩放和反射等，这些变换保持平面内点之间的相对位置关系不变，但可以改变形状、大小和方向。

平面的相交与切割：两个或多个平面相交会形成直线或新的平面区域；而用平面切割立体图形，可以得到截面，截面形状取决于切割方向和立体图形的结构。

平面内的曲线与曲面：尽管平面本身是无曲的，但可以在其上定义各种曲线（如圆、椭圆、抛物线等）和通过映射生成的曲面（如平面上的图形绕一条直线旋转形成的圆柱面）。

平面几何与解析几何的融合：解析几何为平面几何提供了强大的数学工具，如坐标系统、向量运算和方程表示，使得许多复杂的几何问题得以量化分析和精确求解。

六、结语

平面的概念是连接直观感知与抽象思维的桥梁，它不仅是几何学的基础，更是理解物理世界、进行工程设计、创造艺术作品和推动科技进步的重要工具。通过对平面的深入学习，我们不仅能够掌握其定义、性质和应用，还能在探索未知的过程中培养逻辑思维、空间想象能力和创新思维。正如平面本身那样，几何学的学习之旅也是无限宽广、充满可能的。希望本文能激发读者对平面概念的兴趣，引领大家进一步探索几何学的奇妙世界。